何为线段树
线段树是基于要研究的数组而构建的数据结构,呈二叉树状。线段树的叶子结点就是所要研究的数组,非叶子节点表示数组的一段区间的某个性质的值。比如此区间的和,或者最大值最小值等等。
为什么需要线段树呢?试想你需要设计一个功能,给定一个数组,需要你提供两个操作,一是更改某个元素,而是索引某个区间的和,或者最大值,或者最小值,这里以和举例。最直接也是最简单做法当然是直接在数组上操作,O(1)更新,O(N)索引和,N为区间长度。
class NumArray {
public NumArray(int[] nums) { //TODO }
// Updates nums[index] = val.
public void update(int index, int val) { //TODO}
// Gets sum of nums[left ... right].
public int query(int left, int right) { //TODO }
}
再进一步,如果需要更新一个区间的元素呢,比如,nums[i] += val, for left <= i <= right。
class NumArray {
// ...
// Add val, for nums[i] with left <= i <= right
public int add(int left, int right, int val) { //TODO }
}
继续以上方法,就是遍历区间,一一更新,与索引相同复杂度:O(N)。
有没有能索引复杂度的方法?有,线段树就是其中一种,通过构造线段树,可以将索引复杂度降低到O(logN), N为区间长度,但会增加update复杂度到O(logN),N为原数组长度。而一般的应用场景,读远大于写,所以这个改进非常有益于整体性能提升。
那如何构造线段树呢?可以通过数组表示,也可以通过一棵树来表示。先说数组表示法。
基于数组的线段树
给定的研究数组a[],长度为N,线段树用数组tree[]表示,则有:
- 根节点为
tree[0],覆盖数组范围a[0 ... N-1]。 - 根的左孩子
tree[1],覆盖范围是父节点前一半,即a[0 ... N/2]。有孩子tree[2],覆盖范围父节点后一半,即a[N/2 + 1 ... N-1]。 - 上面两步不断重复,即对于节点
tree[i], range[l ... r],令mid=(l+r)/2则有左孩子tree[2*i+1], range[l ... mid],右孩子tree[2*i+2], range[mid+1, r]。 - 如此递归构造知道叶子节点
tree[i], range[l ... r],此时l == r,则令tree[i]=the desired value。
代码如下:
class SegmentTree {
private int[] tree;
private int n;
public SegmentTree(int n) {
this.n = n;
int len = (1 << (1 + (int)(Math.ceil(Math.log(n) / Math.log(2))))) - 1;
tree = new int[len];
}
public int query(int left, int right) {
return queryCore(left, right, 0, n - 1, 0);
}
public void update(int left, int right, int newVal) {
updateCore(left, right, 0, n - 1, 0, newVal);
}
private int queryCore(int left, int right, int segLeft, int segRight, int index) {
if (left > segRight || right < segLeft) {
return 0;
}
if (left <= segLeft && segRight <= right) {
return tree[index];
}
int mid = getMid(segLeft, segRight);
return merge(queryCore(left, right, segLeft, mid, index * 2 + 1),
queryCore(left, right, mid + 1, segRight, index * 2 + 2));
}
private void updateCore(int left, int right,
int segLeft, int segRight, int index, int newVal) {
if (left > segRight || right < segLeft) {
return;
}
if (segLeft == segRight) {
tree[index] = newVal;
return;
}
int mid = getMid(segLeft, segRight);
updateCore(left, right, segLeft, mid, index * 2 + 1, newVal);
updateCore(left, right, mid + 1, segRight, index * 2 + 2, newVal);
tree[index] = merge(tree[2 * index + 1], tree[2 * index + 2]);
}
// Depending on the query, it can be sum, max, min, etc of an interval.
// Here is sum of interval.
private int merge(int leftVal, int rightVal) {
return leftVal + rightVal;
}
private int getMid(int left, int right) {
return left + (right - left) / 2;
}
}
如果给定了一个数组a[],则基于构造此数组的线段树调用方式为:
SegmentTree tree = new SegmentTree(a.length);
for (int i = 0; i < a.lenght; ++i) {
tree.update(i, i, a[i]);
}
结合以上代码与下图可以走一遍构造过程。
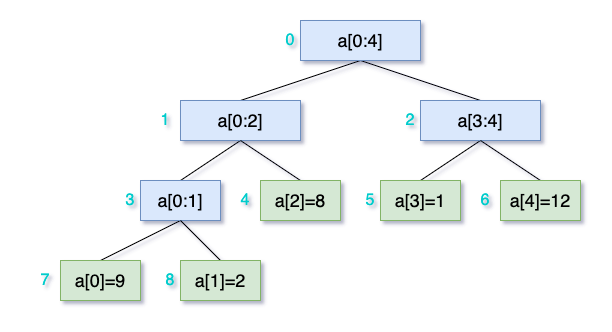
大家可能疑问了,这个tree[]长度为什么这么计算?很简单,可以看到所构造的线段树是一棵完全二叉树,注意不一定满。其叶子节点共有N个,假设最终的深度为h,则有2^h = N,所以h = logN。接下来就是等比求和1+2+4+...+2^h = 2^(1+h) - 1。因为不一定是满二叉树,所以要logN往上取整。这也说明,会有一些节点永远不会被用到而浪费空间。
回顾下用BIT解决的Leetcode 307. Range Sum Query,也可以用线段树来解。代码如下,时间复杂度一致,但空间复杂度线段树更大,不多赘述。
class NumArray {
private SegmentTree tree;
public NumArray(int[] nums) {
tree = new SegmentTree(nums.length);
for (int i = 0; i < nums.length; ++i) {
tree.update(i, i, nums[i]);
}
}
public void update(int index, int val) {
tree.update(index, index, val);
}
public int sumRange(int left, int right) {
return tree.query(left, right);
}
}
基于二叉树的线段树
前面介绍了基于数组的线段树,灵活但不直观。其实看上图就可以推测,完全可以用二叉树来构造线段树。直接上代码,可以看到,基于二叉树后,初始化线段树只需要初始化一个空节点作为根,甚至可以只记录下N,然后用到时再初始化root也行。
class SegmentTree {
private Node root;
public SegmentTree(int N) {
this.root = new Node(0, 0, N - 1);
}
public int query(int left, int right) {
return queryCore(left, right, root);
}
public void update(int left, int right, int newVal) {
updateCore(left, right, root, newVal);
}
private int queryCore(int left, int right, Node cur) {
if (left > cur.high || right < cur.low) {
return 0;
}
if (left <= cur.low && cur.high <= right) {
return cur.val;
}
return merge(queryCore(left, right, cur.left),
queryCore(left, right, cur.right));
}
private void updateCore(int left, int right, Node cur, int newVal) {
if (left > cur.high || right < cur.low) {
return;
}
if (cur.low == cur.high) {
cur.val = newVal;
return;
}
int mid = getMid(cur.low, cur.high);
if (cur.left == null) {
cur.left = new Node(0, cur.low, mid);
}
if (cur.right == null) {
cur.right = new Node(0, mid + 1, cur.high);
}
updateCore(left, right, cur.left, newVal);
updateCore(left, right, cur.right, newVal);
cur.val = merge(cur.left.val, cur.right.val);
}
// Depending on the query, it can be sum, max, min, etc of an interval.
// Here is sum of interval.
private int merge(int leftVal, int rightVal) {
return leftVal + rightVal;
}
private int getMid(int left, int right) {
return left + (right - left) / 2;
}
static class Node {
// The value for range [low ... high].
public int val;
public int low;
public int high;
public Node left = null;
public Node right = null;
public Node(int val, int low, int high) {
this.val = val;
this.low = low;
this.high = high;
}
}
}
线段树的应用
上面举例,线段树都是用于求和,也可用于其他,比如数组区间的最大值,最小值,等等。所需要的修改非常简单,只需要更改merge方法。比如改为针对最大值的线段树,则只需作如下修改:
private int merge(int leftVal, int rightVal) {
return Math.max(leftVal, rightVal);
}
其他一概不动,当然是有前提的,基于索引数组区间的性质,可能需要改动线段树初始化值。比如在求和时,我们把未初始化的节点(或者叫null节点)值默认为0,这是合理的,因为加merge的参数中如果有null节点,则加0对结果没有影响。
如果是求最大值,则初始化时,为了让merge null节点对最终结果没影响,应该很容易想到,null节点默认值应该为MIN,如此max(val, MIN)肯定返回val。
线段树虽然比BIT费空间,但比BIT灵活。记住,多做的功不会白费,总会在某个地方回馈。一碗线段树鸡汤送给你。