懒更新(lazy update)
上文留下一个问题没有解决,就是对一个区间更新。对一个元素的更新复杂度为O(N),N为数组长度,按上文方法对区间更新,则复杂度为L*O(N), L为区间长度。
另外,更新原数组元素,是从线段树中对应的叶子节点,一路向上更新到根节点。如果所要更新的区间有很多公共祖先节点,那么这些节点每次都需要被更新一次。如图中如果我们要更新数组中的2, 8, 6分别+5, +1, +9,可以看到图中公共节点如19会更新2次,37则有3次。
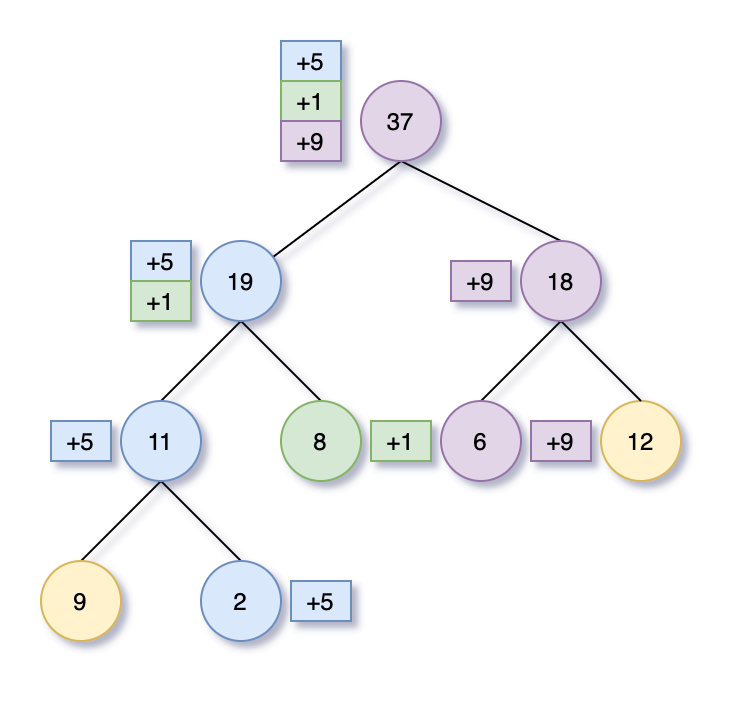
另外,在实际应用中,可能只是某些热点数据会频繁被读取,而大部分数据是在冷宫常年不见天日。有些更新没有必要立即落实到每一个节点,而可以在其被读取时再落实更新。
这就是懒更新的登场时刻。
基于数组的实现
既然需要将更新延后落实,那么就需要保存这些更新,所以需要一个与tree长度一致的lazy数组来保存对应节点没有落实的更新。代码如下。几个注意点:
- 进入
queryCore时,首先需要检查有无当前节点index的更新,如果有,先执行更新,清空该更新,然后继续,其余与正常线段树query区别。 - 进入
updateCore时,也是首先要检查有无当前节点index的更新,如果有,重复上面。 - 另外,当更新范围
[left, right]完全覆盖当前节点代表区间[segLeft, segRight]时,要再次执行更新,但这次update参数是newVal。这是关键点所在,执行完更新,就不用继续递归调用了,因为孩子节点的更新被保存在了lazy[leftChild]和lazy[rightChild]。下次再调用query或者update时,如果执行到节点leftChild或rightChild,则会执行之前保存的更新。
class SegmentTree {
private int[] tree;
private int[] lazy;
private int n;
public SegmentTree(int n) {
this.n = n;
int len = (1 << (1 + (int)(Math.ceil(Math.log(n) / Math.log(2))))) - 1;
tree = new int[len];
lazy = new int[len];
}
public int query(int left, int right) {
return queryCore(left, right, 0, n - 1, 0);
}
public void update(int left, int right, int newVal) {
updateCore(left, right, 0, n - 1, 0, newVal);
}
private int queryCore(int left, int right, int segLeft, int segRight, int index) {
if (lazy[index] != 0) {
// Execute un-merged update.
execute(index, lazy[index], segLeft, segRight);
// Clear merged update.
lazy[index] = 0;
}
if (left > segRight || right < segLeft) {
return 0;
}
if (left <= segLeft && segRight <= right) {
return tree[index];
}
int mid = getMid(segLeft, segRight);
return merge(queryCore(left, right, segLeft, mid, index * 2 + 1),
queryCore(left, right, mid + 1, segRight, index * 2 + 2));
}
private void updateCore(int left, int right,
int segLeft, int segRight, int index, int newVal) {
if (lazy[index] != 0) {
execute(index, lazy[index], segLeft, segRight);
lazy[index] = 0;
}
if (left > segRight || right < segLeft) {
return;
}
if (left <= segLeft && segRight <= right) {
// Execute update for newVal.
execute(index, newVal, segLeft, segRight);
return;
}
int mid = getMid(segLeft, segRight);
updateCore(left, right, segLeft, mid, index * 2 + 1, newVal);
updateCore(left, right, mid + 1, segRight, index * 2 + 2, newVal);
tree[index] = merge(tree[index * 2 + 1], tree[index * 2 + 2]);
}
// Execute an update against tree[index] with interval [segLeft, segRight].
private void execute(int index, int update, int segLeft, int segRight) {
// Apply the udpate.
tree[index] = merge(tree[index], update);
if (segLeft != segRight) {
// Propagate the update to children.
lazy[2 * index + 1] = merge(lazy[2 * index + 1], update);
lazy[2 * index + 2] = merge(lazy[2 * index + 2], update);
}
}
private int merge(int x, int y) {
return Math.max(x, y);
}
private int getMid(int left, int right) {
return left + (right - left) / 2;
}
}
基于树的实现
其实就是把上面的代码做一次翻译,不多赘述。
class SegmentTree {
private Node root;
public SegmentTree(int n) {
this.root = new Node(0, 0, n - 1);
}
public int query(int left, int right) {
return queryCore(left, right, root);
}
public void update(int left, int right, int newVal) {
updateCore(left, right, root, newVal);
}
private int queryCore(int left, int right, Node cur) {
if (cur == null) {
return 0;
}
if (cur.lazyVal != 0) {
// Execute un-merged update.
execute(cur, cur.lazyVal);
// Clear merged update.
cur.lazyVal = 0;
}
if (left > cur.high || right < cur.low) {
return 0;
}
if (left <= cur.low && cur.high <= right) {
return cur.val;
}
return merge(queryCore(left, right, cur.left),
queryCore(left, right, cur.right));
}
private void updateCore(int left, int right, Node cur, int newVal) {
if (cur.lazyVal != 0) {
// Execute un-merged update.
execute(cur, cur.lazyVal);
// Clear merged update.
cur.lazyVal = 0;
}
if (left > cur.high || right < cur.low) {
return;
}
if (left <= cur.low && cur.high <= right) {
// Execute update for newVal.
execute(cur, newVal);
return;
}
int mid = getMid(cur.low, cur.high);
if (cur.left == null) {
cur.left = new Node(0, cur.low, mid);
cur.right = new Node(0, mid + 1, cur.high);
}
updateCore(left, right, cur.left, newVal);
updateCore(left, right, cur.right, newVal);
cur.val = merge(cur.left.val, cur.right.val);
}
private void execute(Node cur, int update) {
// Apply the udpate.
cur.val = merge(cur.val, update);
if (cur.low != cur.high) {
// Propagate the updates to children.
if (cur.left == null) {
int mid = getMid(cur.low, cur.high);
cur.left = new Node(0, cur.low, mid);
cur.right = new Node(0, mid + 1, cur.high);
}
cur.left.lazyVal = merge(cur.left.lazyVal, update);
cur.right.lazyVal = merge(cur.right.lazyVal, update);
}
}
private int merge(int x, int y) {
return Math.max(x, y);
}
private int getMid(int left, int right) {
return left + (right - left) / 2;
}
static class Node {
// The value for range [low ... high].
public int val;
public int low;
public int high;
// The lazy update yet to apply.
public int lazyVal;
public Node left = null;
public Node right = null;
public Node(int val, int low, int high) {
this.val = val;
this.low = low;
this.high = high;
this.lazyVal = 0;
}
}
}
应用
上述线段树都基于一个假设,即数组元素允许最小值为0,所以我们把入门篇里所说的null节点的值默认为0。再次重申,对于不同的区间性质(和,最大,最小等),null节点的默认值需要作相应调整。
基于上面的线段树可以轻松的解决Leetcode 699 Falling Squares,以更低的复杂度!
原题表述较为啰嗦,总结如下。给定一组方块以positions[][]表示,position[i]表示方块i,position[i][0]表示方块在x轴上坐标,position[i][1]表示方块边长。依次把方块从很高处沿y轴扔下,后面的方块有可能掉在前面方块上。
比如:
positions = [[1, 2], [2, 3], [6, 1]]则扔完后会像下图所示。
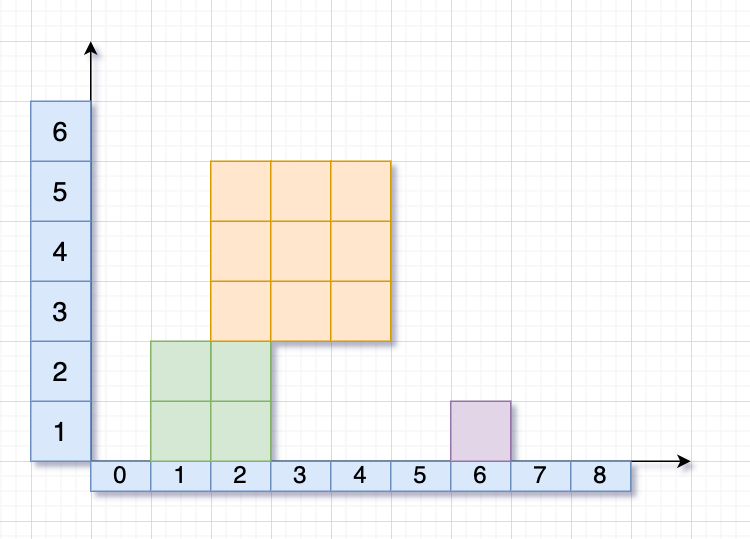
现在要求heights[],heights[i]表示在扔到方块i时,所有已扔方块形成的形状的最高高度。比如上述输入,则结果是[2, 5, 5]。
此题完全可以暴力解决,维持一个heights[]数组来维持到方块i掉下时的高度。
heights[]长度与方块数相同,初始化为0.- 当方块
i掉下时,heights[i] += positions[i][1]。 - 同时需要更新方块
i覆盖范围内的heights[]。 - 取当前最大值作为方块
i掉落时的最高高度。
代码如下:
public List<Integer> fallingSquares(int[][] positions) {
int[] heights = new int[positions.length];
List<Integer> ans = new ArrayList<>();
int cur = 0;
for (int i = 0; i < heights.length; ++i) {
int left = positions[i][0];
int size = positions[i][1];
int right = left + size - 1;
heights[i] += size;
for (int j = i + 1; j < heights.length; ++j) {
int left2 = positions[j][0];
int size2 = positions[j][1];
int right2 = left2 + size2 - 1;
if (left2 <= right && right2 >= left) {
heights[j] = Math.max(heights[i], heights[j]);
}
}
cur = Math.max(cur, heights[i]);
ans.add(cur);
}
return ans;
}
可以看到,上述O(n^2)的算法中,内循环部分是为了找到方块i掉落所覆盖的区域[left ... right]的最大值,线性扫描更新为O(n)。而线段树则能以O(logN)的复杂度query区域[left ... right]的最大值。
在这里,还需要对已有数据进行个小处理,名为坐标压缩,以便于后续线段树构造。所谓坐标压缩,方块的横坐标较为分散,上面的例子里有1, 2, 6三个离散值,可以一一映射到从0开始,间隔1的坐标中,如下图所示。
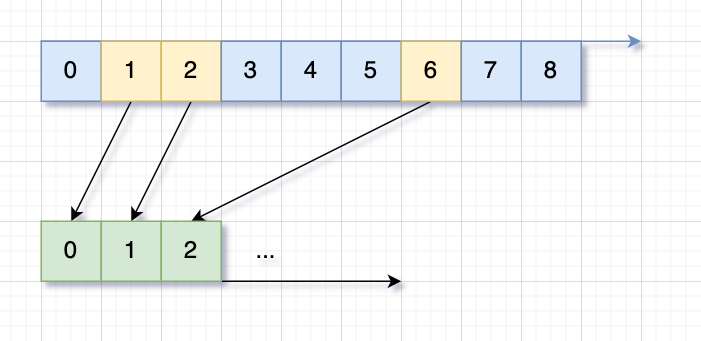
代码实现:
private Map<Integer, Integer> compressCoord(int[][] positions) {
Set<Integer> points = new HashSet<>();
for (int[] pos : positions) {
points.add(pos[0]);
points.add(pos[0] + pos[1] - 1);
}
List<Integer> pointList = new ArrayList<>(points);
Collections.sort(pointList);
Map<Integer, Integer> coords = new HashMap<>();
for (int i = pointList.size() - 1; i >= 0; --i) {
coords.put(pointList.get(i), i);
}
return coords;
}
有了以上铺垫,基于线段树的解法如下:
public List<Integer> fallingSquares(int[][] positions) {
Map<Integer, Integer> coords = compressCoord(positions);
SegmentTree st = new SegmentTree(coords.size());
List<Integer> ans = new ArrayList<>();
int max = 0;
for (int[] pos : positions) {
int left = coords.get(pos[0]);
int right = coords.get(pos[0] + pos[1] - 1);
int height = st.query(left, right) + pos[1];
st.update(left, right, height);
max = Math.max(max, height);
ans.add(max);
}
return ans;
}